

| Financial Toolbox |   |
Simulate a univariate GARCH(P,Q) process with Gaussian innovations
Syntax
Arguments
Description
[U, H] = ugarchsim(Kappa, Alpha, Beta, NumSamples)
simulates a univariate GARCH(P,Q) process with Gaussian innovations.
U is a number of samples (NUMSAMPLES)-by-1 vector of innovations (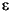 t), representing a mean-zero, discrete-time stochastic process. The innovations time series
t), representing a mean-zero, discrete-time stochastic process. The innovations time series U is designed to follow the GARCH(P,Q) process specified by the inputs Kappa, Alpha, and Beta.
H is a NUMSAMPLES-by-1 vector of the conditional variances (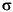 t2) corresponding to the innovations vector
t2) corresponding to the innovations vector U. Note that U and H are the same length, and form a "matching" pair of vectors. As shown in the following equation, 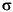 t2 (i.e.,
t2 (i.e., H(t)) represents the time series inferred from the innovations time series {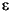 t} (i.e.,
t} (i.e., U).
The time-conditional variance, 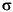 t2, of a GARCH(P,Q) process is modeled as
t2, of a GARCH(P,Q) process is modeled as
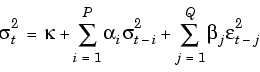
where 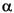 represents the argument
represents the argument Alpha, 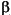 represents
represents Beta, and the GARCH(P,Q) coefficients {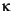 ,
, 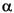 ,
, 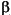 } are subject to the following constraints.
} are subject to the following constraints.
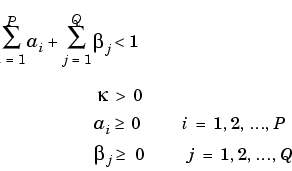
Note that U is a vector of residuals or innovations (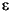 t) of an econometric model, representing a mean-zero, discrete-time stochastic process.
t) of an econometric model, representing a mean-zero, discrete-time stochastic process.
Although 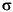 t2 is generated using the equation above,
t2 is generated using the equation above, 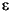 t and
t and 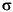 t2 are related as
t2 are related as
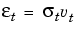
where {vt} is an independent, identically distributed (i.i.d.) sequence ~ N(0,1).
The output vectors U and H are designed to be steady-state sequences in which transients have arbitrarily small effect. The (arbitrary) metric used by ugarchsim strips the first N samples of U and H such that the sum of the GARCH coefficients, excluding Kappa, raised to the Nth power, does not exceed 0.01.
Note
ugarchsim corresponds generally to the GARCH Toolbox function garchsim. The GARCH Toolbox provides a comprehensive and integrated computing environment for the analysis of volatility in time series. For information see the GARCH Toolbox User's Guide or the financial products Web page at http://www.mathworks.com/products/finprod/.
|
Examples
This example simulates a GARCH(P,Q) process with P = 2 and Q = 1.
% Set the random number generator seed for reproducability. randn('seed', 10) % Set the simulation parameters of GARCH(P,Q) = GARCH(2,1) process. Kappa = 0.25; %a positive scalar. Alpha = [0.2 0.1]'; %a column vector of nonnegative numbers (P = 2). Beta = 0.4; % Q = 1. NumSamples = 500; % number of samples to simulate. % Now simulate the process. [U , H] = ugarchsim(Kappa, Alpha, Beta, NumSamples); % Estimate the process parameters. P = 2; % Model order P (P = length of Alpha). Q = 1; % Model order Q (Q = length of Beta). [k, a, b] = ugarch(U , P , Q); disp(' ') disp(' Estimated Coefficients:') disp(' -----------------------') disp([k; a; b]) disp(' ') % Forecast the conditional variance using the estimated % coefficients. NumPeriods = 10; % Forecast out to 10 periods. [VarianceForecast, H1] = ugarchpred(U, k, a, b, NumPeriods); disp(' Variance Forecasts:') disp(' ------------------') disp(VarianceForecast) disp(' ')
When the above code is executed, the screen output looks like the display shown.
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%Diagnostic Information Number of variables: 4 Functions Objective: ugarchllf Gradient: finite-differencing Hessian: finite-differencing (or Quasi-Newton) Constraints Nonlinear constraints: do not exist Number of linear inequality constraints: 1 Number of linear equality constraints: 0 Number of lower bound constraints: 4 Number of upper bound constraints: 0 Algorithm selected medium-scale%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%End diagnostic information max Directional Iter F-count f(x) constraint Step-size derivative Procedure 1 5 699.185 -0.125 1 -2.97e+006 2 22 658.224 -0.1249 0.000488 -64.6 3 28 610.181 0 1 -49.4 4 35 590.888 0 0.5 -38.9 5 42 583.961 -0.03317 0.5 -29.8 6 49 583.224 -0.02756 0.5 -31.8 7 57 582.947 -0.02067 0.25 -7.28 8 63 578.182 0 1 -2.43 9 71 578.138 -0.09145 0.25 -0.55 10 77 577.898 -0.04452 1 -0.148 11 84 577.882 -0.06128 0.5 -0.0488 12 90 577.859 -0.07117 1 -0.000758 13 96 577.858 -0.07033 1 -0.000305 Hessian modified 14 102 577.858 -0.07042 1 -3.32e-005 Hessian modified 15 108 577.858 -0.0707 1 -1.29e-006 Hessian modified 16 114 577.858 -0.07077 1 -1.29e-007 Hessian modified 17 120 577.858 -0.07081 1 -1.97e-007 Hessian modified Optimization Converged Successfully Magnitude of directional derivative in search direction less than 2*options.TolFun and maximum constraint violation is less than options.TolCon No Active Constraints Estimated Coefficients: ---------------------- 0.2520 0.0708 0.1623 0.4000 Variance Forecasts: ------------------ 1.3243 0.9594 0.9186 0.8402 0.7966 0.7634 0.7407 0.7246 0.7133 0.7054
See Also
ugarch, ugarchpred, and the GARCH Toolbox function garchsim
References
James D. Hamilton, Time Series Analysis, Princeton University Press, 1994
 | ugarchpred | weekday |  |