

| Function Reference |   |
Compute the Bode frequency response of LTI models
Syntax
bode(sys) bode(sys,w) bode(sys1,sys2,...,sysN) bode(sys1,sys2,...,sysN,w) bode(sys1,'PlotStyle1',...,sysN,'PlotStyleN') [mag,phase,w] = bode(sys)
Description
bode computes the magnitude and phase of the frequency response of LTI models. When invoked without left-side arguments, bode produces a Bode plot on the screen. The magnitude is plotted in decibels (dB), and the phase in degrees. The decibel calculation for mag is computed as 20log10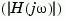 , where
, where 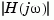 is the system's frequency response. Bode plots are used to analyze system properties such as the gain margin, phase margin, DC gain, bandwidth, disturbance rejection, and stability.
is the system's frequency response. Bode plots are used to analyze system properties such as the gain margin, phase margin, DC gain, bandwidth, disturbance rejection, and stability.
bode(sys) plots the Bode response of an arbitrary LTI model sys. This model can be continuous or discrete, and SISO or MIMO. In the MIMO case, bode produces an array of Bode plots, each plot showing the Bode response of one particular I/O channel. The frequency range is determined automatically based on the system poles and zeros.
bode(sys,w) explicitly specifies the frequency range or frequency points to be used for the plot. To focus on a particular frequency interval [wmin,wmax], set w = {wmin,wmax}. To use particular frequency points, set w to the vector of desired frequencies. Use logspace to generate logarithmically spaced frequency vectors. All frequencies should be specified in radians/sec.
bode(sys1,sys2,...,sysN) or bode(sys1,sys2,...,sysN,w) plots the Bode responses of several LTI models on a single figure. All systems must have the same number of inputs and outputs, but may otherwise be a mix of continuous and discrete systems. This syntax is useful to compare the Bode responses of multiple systems.
bode(sys1,'PlotStyle1',...,sysN,'PlotStyleN') specifies which color, linestyle, and/or marker should be used to plot each system. For example,
uses red dashed lines for the first system sys1 and green 'x' markers for the second system sys2.
When invoked with left-side arguments
return the magnitude and phase (in degrees) of the frequency response at the frequencies w (in rad/sec). The outputs mag and phase are 3-D arrays with the frequency as the last dimension (see "Arguments" below for details). You can convert the magnitude to decibels by
Remark
If sys is an FRD model, bode(sys,w), w can only include frequencies in sys.frequency.
Arguments
The output arguments mag and phase are 3-D arrays with dimensions
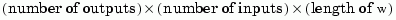
For SISO systems, mag(1,1,k) and phase(1,1,k) give the magnitude and phase of the response at the frequency 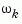 =
= w(k).
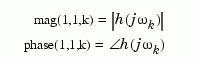
MIMO systems are treated as arrays of SISO systems and the magnitudes and phases are computed for each SISO entry hij independently (hij is the transfer function from input j to output i). The values mag(i,j,k) and phase(i,j,k) then characterize the response of hij at the frequency w(k).
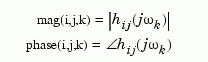
Example
You can plot the Bode response of the continuous SISO system
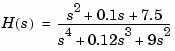
To plot the response on a wider frequency range, for example, from 0.1 to 100 rad/sec, type
You can also discretize this system using zero-order hold and the sample time 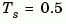 second, and compare the continuous and discretized responses by typing
second, and compare the continuous and discretized responses by typing
Algorithm
For continuous-time systems, bode computes the frequency response by evaluating the transfer function 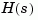 on the imaginary axis
on the imaginary axis 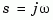 . Only positive frequencies
. Only positive frequencies 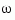 are considered. For state-space models, the frequency response is
are considered. For state-space models, the frequency response is
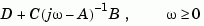
When numerically safe, 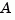 is diagonalized for maximum speed. Otherwise,
is diagonalized for maximum speed. Otherwise, 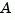 is reduced to upper Hessenberg form and the linear equation
is reduced to upper Hessenberg form and the linear equation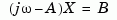 is solved at each frequency point, taking advantage of the Hessenberg structure. The reduction to Hessenberg form provides a good compromise between efficiency and reliability. See [1] for more details on this technique.
is solved at each frequency point, taking advantage of the Hessenberg structure. The reduction to Hessenberg form provides a good compromise between efficiency and reliability. See [1] for more details on this technique.
For discrete-time systems, the frequency response is obtained by evaluating the transfer function 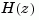 on the unit circle. To facilitate interpretation, the upper-half of the unit circle is parametrized as
on the unit circle. To facilitate interpretation, the upper-half of the unit circle is parametrized as
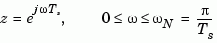
where 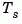 is the sample time.
is the sample time. 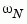 is called the Nyquist frequency. The equivalent "continuous-time frequency"
is called the Nyquist frequency. The equivalent "continuous-time frequency" 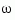 is then used as the
is then used as the 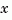 -axis variable. Because
-axis variable. Because
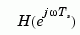
is periodic with period 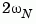 ,
, bode plots the response only up to the Nyquist frequency 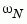 . If the sample time is unspecified, the default value
. If the sample time is unspecified, the default value 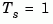 is assumed.
is assumed.
Diagnostics
If the system has a pole on the 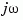 axis (or unit circle in the discrete case) and
axis (or unit circle in the discrete case) and w happens to contain this frequency point, the gain is infinite, 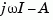 is singular, and
is singular, and bode produces the warning message
See Also
evalfr Response at single complex frequency
freqresp Frequency response computation
ltiview LTI system viewer
nichols Nichols plot
nyquist Nyquist plot
sigma Singular value plot
References
[1] Laub, A.J., "Efficient Multivariable Frequency Response Computations," IEEE Transactions on Automatic Control, AC-26 (1981), pp. 407-408.
 | bandwidth | bodemag |  |