| MATLAB Function Reference |
  |
bvpset
Create/alter boundary value problem (BVP) options structure
Syntax
options = bvpset('name1',value1,'name2',value2,...)
options = bvpset(oldopts'name1',value1,...)
options = bvpset(oldopts,newopts)
bvpset
Description
options = bvpset('name1',value1,'name2',value2,...)
creates a structure options in which the named properties have the specified values. Any unspecified properties have default values. It is sufficient to type only the leading characters that uniquely identify the property. Case is ignored for property names.
options = bvpset(oldopts,'name1',value1,...)
alters an existing options structure oldopts.
options = bvpset(oldopts,newopts)
combines an existing options structure oldopts with a new options structure newopts. Any new properties overwrite corresponding old properties.
bvpset
with no input arguments displays all property names and their possible values.
BVP Properties
These properties are available.
Property
|
Value
|
Description
|
RelTol
|
Positive scalar {1e-3}
|
A relative tolerance that applies to all components of the residual vector. The computed solution 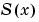 is the exact solution of is the exact solution of
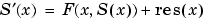 . On each subinterval of the mesh, the residual . On each subinterval of the mesh, the residual 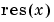 satisfies satisfies
|
AbsTol
|
Positive scalar or vector {1e-6}
|
An absolue tolerance that applies to all components of the residual vector. Elements of a vector of tolerances apply to corresponding components of the residual vector.
|
Vectorized
|
on | {off}
|
Set on to inform bvp4c that you have coded the ODE function F so that F([x1 x2 ...],[y1 y2 ...]) returns [F(x1,y1) F(x2,y2) ...]. That is, your ODE function can pass to the solver a whole array of column vectors at once. This allows the solver to reduce the number of function evaluations, and may significantly reduce solution time.
|
SingularTerm
|
Matrix
|
Singular term of singular BVPs.
Set to the constant matrix S for equations of the form
that are posed on the interval 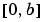 where where 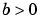 . .
|
FJacobian
|
Function | matrix | cell array
|
Analytic partial derivatives of ODEFUN.
For example, when solving 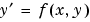 , set this property to , set this property to @FJAC if DFDY = FJAC(X,Y) evaluates the Jacobian of 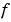 with respect to with respect to 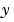 . If the problem involves unknown parameters . If the problem involves unknown parameters 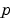 , , [DFDY,DFDP] = FJAC(X,Y,P) must also return the partial derivative of 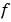 with respect to with respect to 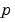 . For problems with constant partial derivatives, set this property to the value of . For problems with constant partial derivatives, set this property to the value of DFDY or to a cell array {DFDY,DFDP}.
|
BCJacobian
|
Function |
cell array
|
Analytic partial derivatives of BCFUN.
For example, for boundary conditions 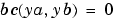 , set this property to , set this property to @BCJAC if [DBCDYA,DBCDYB] = BCJAC(YA,YB) evaluates the partial derivatives of 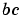 with respect to with respect to 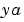 and to and to 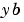 . If the problem involves unknown parameters . If the problem involves unknown parameters 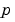 , then , then [DBCDYA,DBCDYB,DBCDP] = BCJAC(YA,YB,P) must also return the partial derivative of 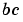 with respect to with respect to 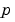 . For problems with constant partial derivatives, set this property to a cell array . For problems with constant partial derivatives, set this property to a cell array {DBCDYA,DBCDYB} or {DBCDYA,DBCDYB,DBCDP}.
|
Nmax
|
positive integer {floor(1000/n)}
|
Maximum number of mesh points allowed.
|
Stats
|
on | {off}
|
Display computational cost statistics.
|
See Also
@ (function_handle), bvp4c, bvpget, bvpinit, deval
 | bvpinit | | bvpval |  |





